Sommes, Gauss et compagnie #1
Le 23 février 2018 (date où j'écris cet article) est l'anniversaire du décès du grand mathématicien allemand Carl Friedrich Gauss, enfin, d'après Wikipédia.

Ayant vécu de 1777 à 1855, il était astronome de métier, mais avait pour principale passion les mathématiques, qu'il révolutionna : en géométrie, par la construction d'un polygone régulier à 17 côtés et en découvrant en partie les géométries non euclidiennes mais surtout en arithmétique, en fondant cette branche des mathématiques sous un socle solide, apportant des définitions rigoureuses des congruences (notamment dans son oeuvre Disquisitiones arithmeticae), en plus d'avoir conjecturé une approximation du nombre de nombres premiers inférieurs à une quantité donnée (la fonction π, mais c'est une autre histoire).
Pour son hommage, nous allons raconter une des anecdotes les plus célèbres de ce dernier. Il était prodige à son plus jeune âge, et cela lui a valu le nom de "Prince des mathématiques".
Il n'a que 7 ans. Alors que son professeur était énervé par l'agitation de la classe, il leur posa un problème au tableau :
Calculer 1+2+3+4+5+6+...+98+99+100.
Trente secondes après, le jeune Gauss trouva la solution : 5050. Mais pourquoi 5050 ???
Voici l'astuce : Il faut renverser la somme :
1+ 2 + 3 + 4 +...+98+99+100
+100+98+99+98+...+ 3 + 2 + 1
101+101+101+101+...+101+101+101
Et combien y a t-il de 101 ? Cent, puisqu'il y a cent termes dans chacune des sommes.
101×100 = 10100. Mais 10100, c'est deux fois la somme. Donc, on a
2×(1+2+3+4+...+98+99+100)=10100
1+2+3+..+98+99+100=10100÷2 = 5050.
On peut généraliser cela.
Théorème. Soit n un entier strictement positif. Alors,
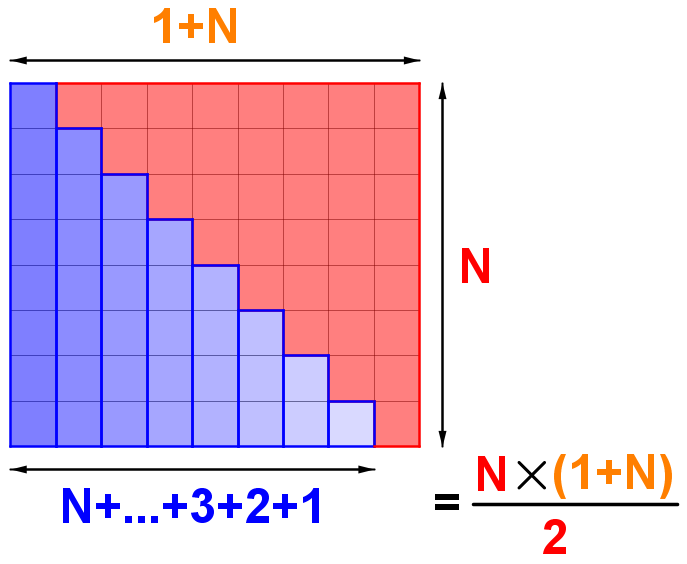
Ce théorème se démontre facilement par récurrence. Mais on peut avoir une vision plus géométrique de cela :
Cela montre que l'on peut voir 1+2+3+4+...+98+99+100 comme un triangle. Appelons T(n) le nombre égal à 1+2+3+...+98+99+100. On peut dire que T(n) est le n-ième nombre triangulaire (puisque ces nombres peuvent être géométriquement représentés comme des triangles équilatéraux)
On a donc T(n)=n(n+1)/2
Théorème. Soit n un entier strictement positif. Alors,
Démonstration. On sait exprimer T(n) en fonction de n
Autrement dit, deux nombres triangulaires consécutifs ont pour somme un carré parfait. Réciproquement, tout carré parfait supérieur ou égal à 4 s'exprime sous somme de deux nombres triangulaires.
Passons à une situation plus concrète. Imaginons un tournoi de n'importe quel sport individuel (sans équipe). Dans ce tournoi, il y a 50 joueurs. Chaque joueur doit affronter chacun des autres joueurs en duel dans un match pour chacun des autres joueurs. Combien y aura-t-il de matchs ?
Numérotons chaque joueur, de J1 à J50.
J1 doit affronter tous les joueurs de J2 à J50 : Il y en a 49.
J2 doit affronter tous les joueurs de J3 à J50, car il a déjà affronté J1 et ne peut s'affronter lui-même : Il doit en affronter 48.
J3 doit affronter de la même manière tous les joueurs de J4 à J50 : 47.
etc...
Le nombre d'affrontements est donc de 1+2+3+...+47+48+49 = 1225.
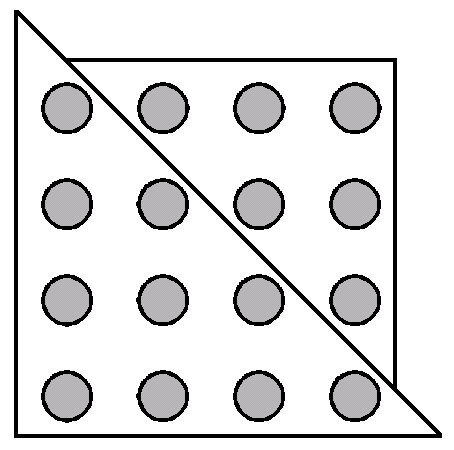
On peut également interpréter cela comme le nombre d'arêtes d'un graphe (un graphe, grossièrement, est un ensemble de points appelés sommets pouvant être reliés par des arêtes) à 50 sommets. Pour simplifier, on va prendre un graphe à 8 sommets. Il y a alors 28 arêtes :
On peut aussi remarquer que T(n) est le nombre de manières de placer deux cavaliers de même couleur dans un échiquier de (n+1)² cases.
En effet, si l'on prend un échiquier classique de 64 cases. On pose le premier cavalier dans l'une des 64 cases. Alors, il reste 63 possibilités pour le deuxième. On pose le premier cavalier dans l'une des 63 autres cases, il y a alors 62 possibilités (63 moins la case déjà occupée par l'autre cavalier avant).
Il y a donc 63+62+61+...+1 = 2016 manières de placer deux cavaliers dans 64 cases différentes.
En fait, si l'on raisonne de manière combinatoire, le nombre de manières de placer deux cavaliers de même couleur dans un échiquier de n+1 cases est le nombre de choix de deux cases que l'on peut faire sur n+1 cases.
Mais sur n+1 cases, on peut choisir d'abord la première, puis la seconde.
Dans ce cas, on a d'abord n+1 choix pour la première, et n pour la seconde. On en a alors n(n+1), sauf que l'ordre ne compte pas, puisque les deux cavaliers sont indentiques.
Or, pour un choix de deux cases, disons AB, combien y a-t-il de choix possibles, si l'on compte l'ordre ? Il y en a deux : AB et BA. Il faut donc diviser le résultat par 2, ce qui donne n(n+1)/2, soit le n-ième nombre triangulaire. C'est fou, non ?
En fait, c'est normal, cela vient du fait que

pour tout n≥ 2. Si vous ne comprenez pas, ce n'est pas grave. On en reparlera dans un futur article.
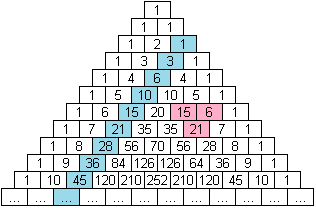
Maintenant, construisons un triangle de nombres spécial (appelé le triangle de Pascal). On part de 1, on ajoute deux 1 aux extrémités de la ligne suivante. Ensuite, chaque nombre est égal à la somme des nombres au dessus, et on continue. Cela donne :

On voit que les nombres triangulaires se situent dans une diagonale...ici, la ligne bleue.
Mais pourquoi ? C'est une autre histoire...que l'on verra dans un futur article.
Sources et liens utiles
2015+1(Cette nouvelle année est-elle intéressante ? Episode 07)
http://eljjdx.canalblog.com/archives/2016/01/03/33119338.html
Un article sur les propriétés du nombre 2016 (écrit le 3 janvier 2016, peu après le Nouvel An donc), mentionnant justement les nombres triangulaires dont on a parlé.
Carl Friedrich Gauss
https://fr.wikipedia.org/wiki/Carl_Friedrich_Gauss
L'article Wikipédia sur Carl Friedrich Gauss